Best Digital SAT Math Prep: "Equivalent Expressions"

Frontier Lesson: "Equivalent Expressions" for the Digital SAT

"Equivalent Expressions" is a skill that falls under the "Advanced Math" domain. While it may sound intimidating at first, it's actually one of the more manageable parts of the SAT math section. By focusing on basic rules of algebra and key strategies for simplifying or rewriting expressions, you can confidently solve these problems.

Essentially, "equivalent expressions" refers to the process of rewriting a mathematical expression into another form that has the same value for all valid inputs. Unlike some other problem types on the SAT, questions in this topic do not involve solving equations or finding the value of variables. Instead, the task is simpler: transform or rearrange the given mathematical expression into an equivalent form. The question prompt often starts with "Which expression is equivalent to...," making it clear that the goal is to modify the expression without altering its meaning.

On the SAT, most "Equivalent Expressions" questions are presented in multiple-choice format, offering four possible answer choices. This is good news! Having pre-set answers means you can often verify your work quickly and confirm whether you've chosen the correct form.

In terms of difficulty, the majority of these problems fall within the easy to moderate range, meaning they are very approachable for well-prepared students. Even the "hard" questions in this category are rarely very difficult. A strong understanding of techniques like factoring, expanding, and simplifying polynomials will allow you to consistently earn points here.

🎯 The "Equivalent Expressions" questions reward precision and mastery of basic algebraic manipulation techniques, such as:

Applying the distributive property
Factoring polynomials (e.g., difference of squares, grouping, or common factors)
Combining like terms
Simplify rational expressions

How to Factor Quadratic and Polynomial Expressions?

Factoring quadratic expressions is a fundamental skill when tackling "Equivalent Expressions" problems on the SAT. In this section, we'll break down the essential steps and techniques to factor quadratics effectively.

🟠 Step 1: If possible, reduce the coefficient of $x^{2}$ to 1

Before factoring, try to simplify the equation by factoring out the greatest common factor (GCF) of all the terms. For example:

Given the quadratic $5 x^{2} - 10 x + 25$ , notice that $5$ is a common factor for all terms. Factor out $5$ :

5 x^{2} - 10 x + 25 = 5 (x^{2} - 2 x + 5)

Now, focus on factoring $x^{2} - 2 x + 5$ within the parentheses.

🎯 Key Insight: In many SAT problems, you may encounter quadratics where the coefficient of $x^{2}$ cannot be easily reduced. In those cases, you will factor directly (covered below). Always look out for common factors first as they simplify the process—but they are not always present.

🟠 Step 2a: Factor $x^{2} + b x + c$ (when the coefficient of $x^{2} = 1$ )

When the coefficient of $x^{2}$ is 1, factor by finding two numbers that:

Multiply to $c$ (the constant term), and
Add to $b$ (the coefficient of $x$ ).

Example: Factor $x^{2} + 5 x + 6$ :

The constant term is $c = 6$ . The coefficient of $x$ is $b = 5$ .
Find two numbers that multiply to $6$ and add to $5$ :

These numbers are $2$ and $3$ , because $2 \times 3 = 6$ and $2 + 3 = 5$ .

So:

x^{2} + 5 x + 6 = (x + 2) (x + 3)

🟠 Step 2b: Factor $a x^{2} + b x + c$ (when the coefficient of $x^{2}$ is not 1)

When the coefficient of $x^{2}$ , $a$ , is not 1, use the grouping method for factoring.

Multiply $a \cdot c$ .
Find two numbers that:

Multiply to $a \cdot c$ , and
Add to $b$ .
1. Rewrite $b x$ as the sum of two terms using these values, and group terms in pairs.

Factor out the greatest common factor (GCF) from each group.
Rewrite as a product of two binomials.

Example: Factor $6 x^{2} + 11 x + 4$ :

Multiply $a \cdot c = 6 \cdot 4 = 24$ .
Find two numbers that multiply to $24$ and add to $11$ : These are $8$ and $3$ .
Rewrite $11 x$ as $8 x + 3 x$ :

6 x^{2} + 11 x + 4 = 6 x^{2} + 8 x + 3 x + 4

Group terms:

(6 x^{2} + 8 x) + (3 x + 4)

Factor out the GCF from each group:

2 x (3 x + 4) + 1 (3 x + 4)

Rewrite as:

(2 x + 1) (3 x + 4)

🎯 Tip: Practice recognizing the numbers that fit the criteria for both factoring $b$ and grouping. Mastery here is key for efficiency on the SAT!

🟠 Special Factoring Rules

Some expressions are easier to factor because they follow special patterns. Knowing these rules will save you time and effort on the test. Let's review and break down the most common types.

➤ (a) Square of a Sum

a^{2} + 2 ab + b^{2} = (a + b)^{2}

The first term is a perfect square, $a^{2}$ .
- The last term is also a perfect square, $b^{2}$ .
The middle term must equal $2 ab$ .

Example:

Factor $x^{2} + 6 x + 9$ :

Identify $a = x$ and $b = 3$ ( $3^{2} = 9$ ).
Verify $6 x = 2 ab = 2 (x) (3)$ .
Rewrite as:

x^{2} + 6 x + 9 = (x + 3)^{2}

➤ (b) Square of a Difference

a^{2} - 2 ab + b^{2} = (a - b)^{2}

Similar to the square of a sum, except the middle term has $- 2 ab$ .

Example:

Factor $4 x^{2} - 12 x + 9$ :

Identify $a = 2 x$ and $b = 3$ ( $3^{2} = 9$ , $(2 x)^{2} = 4 x^{2}$ ).
Verify $- 12 x = - 2 (2 x) (3)$ .
Rewrite as:

4 x^{2} - 12 x + 9 = (2 x - 3)^{2}

➤ (c) Difference of Squares

a^{2} - b^{2} = (a + b) (a - b)

This applies when an expression contains the difference of two perfect squares.

Example:

Factor $x^{2} - 16$ :

Identify $a = x$ and $b = 4$ ( $4^{2} = 16$ ).
Rewrite as:

x^{2} - 16 = (x + 4) (x - 4)

Example 2:

Factor $9 x^{2} - 25 y^{2}$ :

Recognize both $9 x^{2} = (3 x)^{2}$ and $25 y^{2} = (5 y)^{2}$ .
Rewrite as:

9 x^{2} - 25 y^{2} = (3 x + 5 y) (3 x - 5 y)

🎯 Tip: Always check if an expression is a difference of squares, as this is a common pattern tested on the SAT.

➤ Final Steps for Factoring Quadratics

Factor out common terms first. Simplify whenever possible.
Recognize patterns. Identify if the quadratic fits special factoring forms.
Test your work. Multiply your binomials back to verify equivalence.
Watch for SAT traps. Be cautious of answer choices that seem correct but don't fully simplify.

🟠 Common Integer Square Table

Memorize them and enhance your sensitivity to the square and root of numbers, which is very useful for increasing your problem-solving speed and efficiency in real SAT.

Single-digit Integers and Their Squares	Integers Between 10 and 20 and Their Squares
$1 \times 1 = 1$	$10 \times 10 = 100$
$2 \times 2 = 4$	$11 \times 11 = 121$
$3 \times 3 = 9$	$12 \times 12 = 144$
$4 \times 4 = 16$	$13 \times 13 = 169$
$5 \times 5 = 25$	$14 \times 14 = 196$
$6 \times 6 = 36$	$15 \times 15 = 225$
$7 \times 7 = 49$	$16 \times 16 = 256$
$8 \times 8 = 64$	$17 \times 17 = 289$
$9 \times 9 = 81$	$18 \times 18 = 324$
	$19 \times 19 = 361$
	$20 \times 20 = 400$

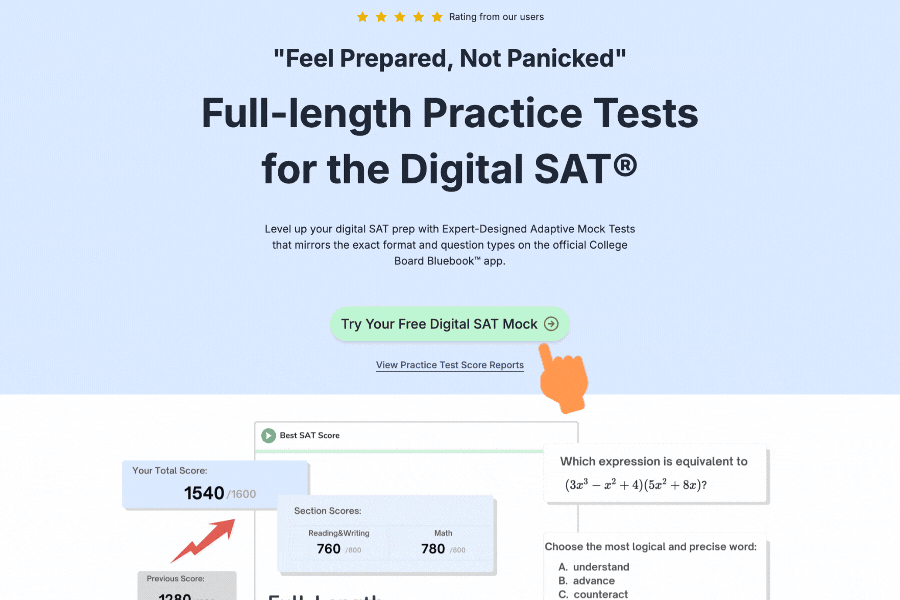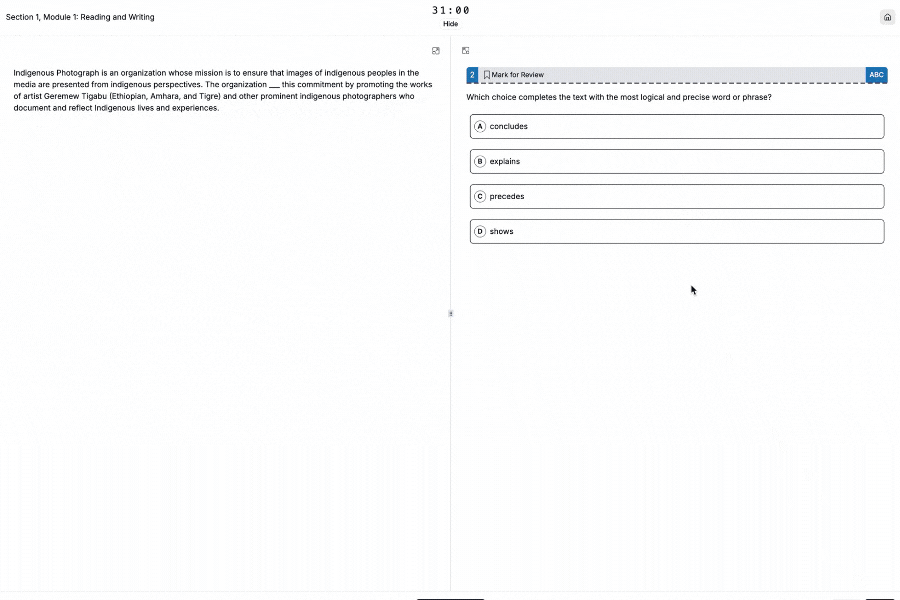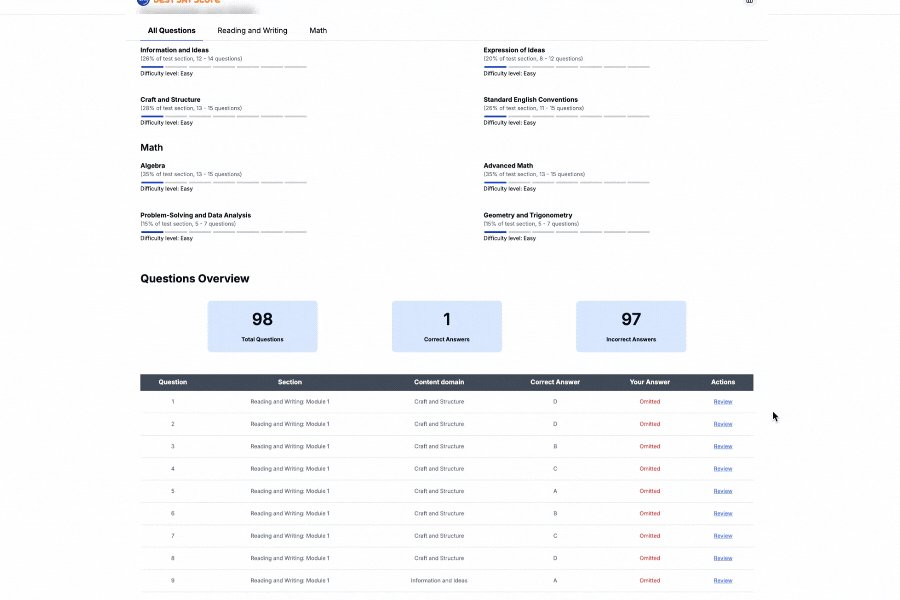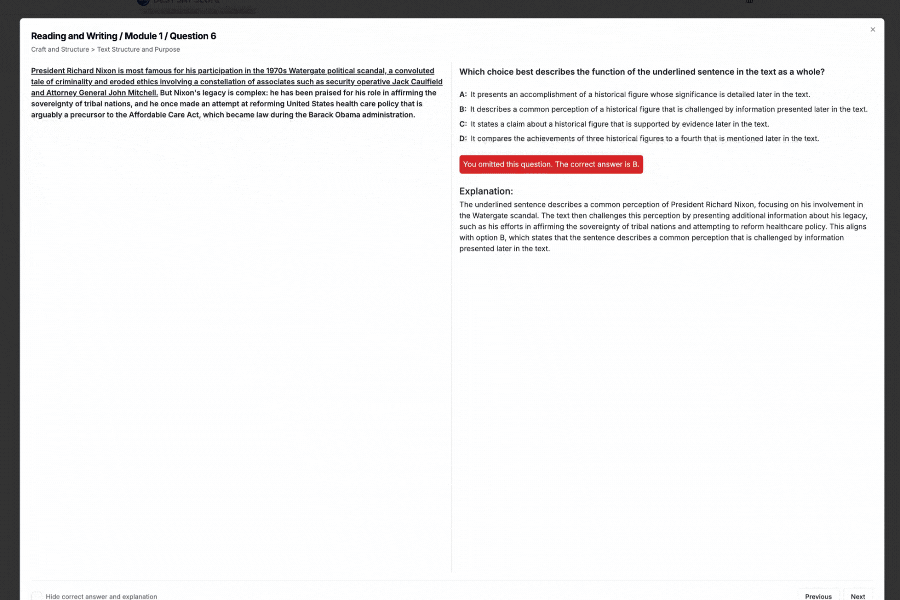
Free Full Length SAT Tests withOfficial-StyleQuestions

Practice with our full length adapive full testreal test-likequestions and proven300+points score boost

Exponential Expressions & Operations with Polynomials

🟠 Common Types of Polynomials in SAT Questions:

A polynomial is an expression consisting of one or more terms. Each term may include a coefficient, a variable base, and an exponent.

Monomial: A polynomial with a single term. Example: $5 x^{3}$ , $- 7 y$ , $30$
Binomial: A polynomial with two terms. Example: $x^{2} - 3 x$ , $5 y + 2$ , $x^{3} - 11 x^{2}$
Trinomial: A polynomial with three terms. Example: $x^{2} + 2 x - 1$ , $3 y^{3} - 4 y + 6$

🟠 How to Add or Subtract Polynomials

Polynomials can be added or subtracted by combining like terms, sharing the same rules of exponent pperations.

➤ a. Combine Like Terms

Definition: "Like terms" share the same variable base AND the same exponent.

You can obly combine: Terms with matching variable bases and exponents. Example: $3 x^{2} + 2 x^{2} = 5 x^{2}$
You cannot combine: Terms with different variable bases or exponents. Example: $3 x^{3} + 5 x^{2} \neq = 8 x^{5}$ (cannot be simplified further).

Try: combine like terms to simplify $2 x^{2} - 5 x + 3 + 4 x^{2} + 6 x - 1$

Key: $(2 x^{2} + 4 x^{2}) + (- 5 x + 6 x) + (3 - 1) = 6 x^{2} + x + 2$

➤ b. Combine Only the Coefficients

When combining like terms, only the coefficients change. The variable base and exponent remain the same.

For example:

4 x^{3} - 7 x^{3} = (4 - 7) x^{3} = - 3 x^{3}

➤ c. Be Mindful of Parentheses and Signs

When adding or subtracting polynomials in parentheses, ensure that you correctly distribute any negative sign across terms.

Example 1:

Simplify $(3 x^{2} + 2 x - 5) - (x^{2} - x + 4)$ :

Distribute the negative sign:

(3 x^{2} + 2 x - 5) - x^{2} + x - 4

Then combine like terms:

(3 x^{2} - x^{2}) + (2 x + x) + (- 5 - 4) = 2 x^{2} + 3 x - 9

➤ d. Write Expressions in Descending Order of Exponents

After combining terms, arrange polynomial terms in order from the highest power of the variable to the lowest.

Example: reorder $5 x - x^{3} - 3 + 2 x^{2}$ :

- x^{3} + 2 x^{2} + 5 x - 3

🟠 How to Multiply Polynomials

The process for multiplying polynomials involves distributing each term of one polynomial to all the terms of the other.

➤ a. Distribute Terms When Multiplying Polynomials

When multiplying two polynomials, multiply each term in one polynomial by each term in the other polynomial.

Example: Multiply $2 x (3 x + 4)$ :

2 x \cdot 3 x + 2 x \cdot 4 = 6 x^{2} + 8 x

➤ b. Use the FOIL Method for Binomials

When multiplying two binomials, you can use FOIL to systematically account for all four products:

(a x + b) (c x + d)

FOIL Steps:

F (First): Multiply the first terms: $a x \cdot c x = a c x^{2}$
O (Outer): Multiply the outer terms: $a x \cdot d = a d x$
I (Inner): Multiply the inner terms: $b \cdot c x = b c x$
L (Last): Multiply the last terms: $b \cdot d$

**Then, combine the results. For example, for $(2 x + 3) (x - 4)$ :

First: $2 x \cdot x = 2 x^{2}$
Outer: $2 x \cdot (- 4) = - 8 x$
Inner: $3 \cdot x = 3 x$
Last: $3 \cdot (- 4) = - 12$

Final result:

2 x^{2} - 8 x + 3 x - 12 = 2 x^{2} - 5 x - 12

➤ c. Multiplying Terms with the Same Base

When multiplying terms that have the same base, apply these rules:

Multiply the coefficients.
Keep the base the same.
Add the exponents.

Example 1:

(2 x^{3}) (4 x^{2}) = (2 \cdot 4) x^{3 + 2} = 8 x^{5}

Example 2:

(5 x^{2}) (3) = (5 \cdot 3) x^{2} = 15 x^{2}

🎯 Tips: Always simplify your final expression and write the terms in descending order of exponents.

🟠 What Is an Exponential Expression?

An exponential expression is any expression where a number or a variable is raised to a power (exponent).

Example: In the expression $- 2 x^{5}$ :

$- 2$ is the coefficient (the numerical factor).
$x$ is the base (the repeated factor).
$5$ is the exponent (the number of times the base is multiplied by itself).

Important Difference Between $- 2 x^{5}$ and $(- 2 x)^{5}$

$- 2 x^{5}$ : The exponent $5$ applies only to $x$ , so:

- 2 x^{5} = - 2 (x \cdot x \cdot x \cdot x \cdot x)

$(- 2 x)^{5}$ : The entire expression $(- 2 x)$ is raised to the 5th power, meaning both $- 2$ and $x$ are multiplied by themselves five times:

(- 2 x)^{5} = (- 2)^{5} \cdot x^{5} = - 32 x^{5}

🎯 Tip: Parentheses are critical! Always consider what the exponent applies to, and interpret expressions carefully!

🟠 The Rules of Exponent Operations

For all the rules below, the base can represent either a number or a variable, and they apply the same way to integer or fractional (rational) exponents.

➤ a. Adding and Subtracting Exponential Expressions

You can add or subtract exponential expressions only if they have the same base with the same exponent.

Example:

3 x^{2} + 5 x^{2} = 8 x^{2}

7 x^{3} - 2 x^{3} = 5 x^{3}

You cannot combine terms with different exponents or bases:

Example: $4 x^{2} + 3 x^{3} \neq = 7 x^{5}$ (it cannot be combined further).

➤ b. Multiplying Exponential Expressions

When multiplying exponential expressions with the same base, keep the base the same and add the exponents.

Rule:

a^{m} \cdot a^{n} = a^{m + n}

Example:

x^{3} \cdot x^{4} = x^{3 + 4} = x^{7}

➤ c. Dividing Exponential Expressions

When dividing exponential expressions with the same base, keep the base the same and subtract the exponents (top exponent minus bottom exponent).

Rule:

\frac{a ^{m}}{a ^{n}} = a^{m - n}, where a \neq = 0

Example 1:

\frac{x ^{5}}{x ^{2}} = x^{5 - 2} = x^{3}

Example 2:

If the terms have coefficients, divide the coefficients and apply the rule to the exponents:

\frac{8 x ^{6}}{4 x ^{3}} = \frac{8}{4} \cdot \frac{x ^{6}}{x ^{3}} = 2 x^{6 - 3} = 2 x^{3}

➤ d. Raising an Exponential Expression to an Exponent

When raising an exponential expression to another exponent, multiply the exponents.

Rule:

(a^{m})^{n} = a^{m \cdot n}

Examples:

(x^{3})^{4} = x^{3 \cdot 4} = x^{12}

(2 x^{2})^{3} = (2^{3}) (x^{2 \cdot 3}) = 8 x^{6}

➤ e. Negative Exponents

Negative exponents represent the reciprocal of the base raised to the corresponding positive exponent.

Rule:

a^{- n} = \frac{1}{a ^{n}}, for a \neq = 0

Examples:

x^{- 3} = \frac{1}{x ^{3}}

(2 x)^{- 2} = \frac{1}{( 2 x ) ^{2}} = \frac{1}{4 x ^{2}}

➤ f. Zero Exponent

Any nonzero base raised to the power of zero equals 1.

Rule:

a^{0} = 1, for a \neq = 0

Examples:

5^{0} = 1, x^{0} = 1, (- y^{2})^{0} = 1, - 8 x^{0} = - 1

➤ g. Rewriting Roots as Rational Exponents

Radical expressions (roots) can be rewritten as rational (fractional) exponents. This is particularly helpful for simplifying expressions with roots.

Rule for Square Root:

x = x^{\frac{1}{2}}

Rule for Higher Roots:

n x^{m} = x^{\frac{m}{n}}

Here:

$m$ is the exponent under the radical (inside the root).
$n$ is the root (the value to the left of ).

Examples:

Square root:

x^{3} = x^{\frac{3}{2}}

Cube root:

3 x^{2} = x^{\frac{2}{3}}

General example:

4 x^{5} = x^{\frac{5}{4}}

How to Do Operations with Rational Expressions

🟠 What Are Rational Expressions?

A rational expression is a fraction where the numerator or denominator (or both) are polynomials. In other words, it represents the division of one polynomial by another.

Examples:

\frac{1}{x}, \frac{x ^{2} + 2 x + 1}{x - 1}, \frac{3 x}{x ^{2} - 4}

Key Note:

The skills required for working with rational expressions (factoring, distributing, combining terms, etc.) are based on everything we've covered earlier about working with polynomial and exponential expressions.

🟠 How to Simplify Rational Expressions

Simplifying rational expressions is similar to simplifying fractions: factor both the numerator and the denominator and cancel any common factors.

Steps to Simplify a Rational Expression:

Factor the numerator and denominator completely.
Cancel common factors that appear in both the numerator and the denominator.
Write the resulting expression.

Example: Simplify $\frac{x ^{2} - 4}{x + 2}$ :

Factor the numerator: $x^{2} - 4 = (x + 2) (x - 2)$
Rewrite: $\frac{( x + 2 ) ( x - 2 )}{x + 2}$
Cancel the common factor $(x + 2)$ :

\frac{( x + 2 ) ( x - 2 )}{x + 2} = x - 2, x \neq = - 2

⚠️ Important: Always state any values of the variable that would make the original denominator equal to zero as restrictions (here, $x \neq = - 2$ ).

🟠 How to Add or Subtract Rational Expressions

Adding and subtracting rational expressions follows the same rules as fractions:

Make sure the denominators are the same (common denominator).
Add or subtract the numerators.
Simplify if possible.

When the denominators are different, you need to find a common denominator (usually the least common multiple, LCM). In most cases, multiplying the two denominators together is the simplest way to find this.

Example: Add $\frac{1}{x} + \frac{2}{x + 1}$ :

Multiply the denominators: $x (x + 1)$
Rewrite both fractions with the common denominator:

\frac{1}{x} = \frac{x + 1}{x ( x + 1 )}, \frac{2}{x + 1} = \frac{2 x}{x ( x + 1 )}

Add the numerators:

\frac{x + 1}{x ( x + 1 )} + \frac{2 x}{x ( x + 1 )} = \frac{( x + 1 ) + 2 x}{x ( x + 1 )}

Simplify:

\frac{x + 1 + 2 x}{x ( x + 1 )} = \frac{3 x + 1}{x ( x + 1 )}

Note: You cannot combine rational expressions until they have the same denominator. Carefully distribute and simplify when expanding numerators.

🟠 How to Multiply or Divide Rational Expressions

Multiplication and division of rational expressions use the same rules as with fractions.

➤ a. Multiplying Rational Expressions

When multiplying two rational expressions:

Factor all terms in the numerators and denominators.
Multiply the numerators and denominators.
Cancel common factors.

Example: Multiply $\frac{x ^{2} + 2 x}{3 x} \cdot \frac{9 x}{x + 2}$ :

Factor the numerator and denominator where possible:

\frac{x ( x + 2 )}{3 x} \cdot \frac{9 x}{x + 2}

Multiply the fractions:

\frac{x ( x + 2 ) \cdot 9 x}{3 x \cdot ( x + 2 )}

Cancel the common factors $(x + 2)$ and $x$ :

\frac{9 x}{3} = 3 x, x \neq = 0, x \neq = - 2

➤ b. Dividing Rational Expressions

Dividing one rational expression by another is equivalent to multiplying by the reciprocal:

\frac{A}{B} \div \frac{C}{D} = \frac{A}{B} \cdot \frac{D}{C}

Example: Divide $\frac{x}{x + 3} \div \frac{x + 1}{x ^{2}}$ :

Rewrite as multiplication by the reciprocal:

\frac{x}{x + 3} \cdot \frac{x ^{2}}{x + 1}

Multiply:

\frac{x \cdot x ^{2}}{( x + 3 ) ( x + 1 )} = \frac{x ^{3}}{( x + 3 ) ( x + 1 )}

➤ c. Factor First to Simplify Multiplication and Division

It is almost always faster and cleaner to factor and cancel first before writing the expanded form of the expression.

Example: Simplify $\frac{x ^{2} - 4}{x ^{2} + 3 x} \cdot \frac{3 x}{x - 2}$ :

Factor:

\frac{( x + 2 ) ( x - 2 )}{x ( x + 3 )} \cdot \frac{3 x}{x - 2}

Cancel $(x - 2)$ and $x$ :

\frac{3 ( x + 2 )}{x + 3}, x \neq = - 2, x \neq = 0, x \neq = - 3

🟠 How to Rewrite Rational Expressions as Quotients and Remainders

When the degree of the numerator is higher than or equal to the degree of the denominator, you can rewrite the rational expression in the form of a quotient and remainder:

q (x) + \frac{r ( x )}{b ( x )}, where r (x) is the remainder.

The process involves polynomial long division.

Example: Rewrite $\frac{x ^{2} + 3 x - 9}{x - 2}$ :

Use polynomial long division:

Divide $x^{2} + 3 x - 9$ by $x - 2$

First term: $(x^{2}) \div (x)$ : $x$

Multiply: $x (x - 2) = x^{2} - 2 x$

Subtract: $(x^{2} + 3 x - 9) - (x^{2} - 2 x) = 5 x - 9$

Second term: $(5 x) \div (x)$ : $5$

Multiply: $5 (x - 2) = 5 x - 10$

Subtract: $(5 x - 9) - (5 x - 10) = 1$

Write the result as:

x + 5 + \frac{1}{x - 2}

Here, $q (x) = x + 5$ , $r (x) = 1$ , $b (x) = x - 2$ .

🎯 Tip: Rewriting expressions in quotient-remainder form is especially helpful for understanding how polynomials behave in division problems.

Worksheet for Building Mastery in Algebraic Operations

Example 1

Task:

Factor $3 x^{2} + 11 x + 6$

Solution:

Identify $a = 3$ , $b = 11$ , $c = 6$ .
Find two numbers that multiply to $a \cdot c = 18$ and add to $b = 11$ : the numbers are $9$ and $2$ .
Rewrite the middle term $11 x$ as $9 x + 2 x$ :

3 x^{2} + 9 x + 2 x + 6

Group terms and factor each group:

3 x (x + 3) + 2 (x + 3)

Factor the common binomial $(x + 3)$ :

(3 x + 2) (x + 3)

Final Answer:

$(3 x + 2) (x + 3)$

Example 2

Task:

Factor $2 x^{2} - 3 x - 5$

Solution:

Identify $a = 2$ , $b = - 3$ , $c = - 5$ .
Find two numbers that multiply to $a \cdot c = - 10$ and add to $b = - 3$ : the numbers are $- 5$ and $2$ .
Rewrite the middle term $- 3 x$ as $- 5 x + 2 x$ :

2 x^{2} - 5 x + 2 x - 5

Group terms and factor each group:

x (2 x - 5) + 1 (2 x - 5)

Factor the common binomial $(2 x - 5)$ :

(x + 1) (2 x - 5)

Final Answer:

$(x + 1) (2 x - 5)$

Example 3

Task:

Simplify $\frac{x ^{2} - 25}{x ^{2} + 10 x + 25}$

Solution:

Recognize that $x^{2} - 25$ is a difference of squares:

x^{2} - 25 = (x - 5) (x + 5)

Recognize that $x^{2} + 10 x + 25$ is a perfect square trinomial:

x^{2} + 10 x + 25 = (x + 5) (x + 5) = (x + 5)^{2}

Simplify the fraction by canceling one factor of $(x + 5)$ :

\frac{( x - 5 ) ( x + 5 )}{( x + 5 ) ^{2}} = \frac{x - 5}{x + 5}

Final Answer:

$\frac{x - 5}{x + 5}, x \neq = - 5$

Example 4

Task:

Factor $36 x^{2} + 36 x + 9$

Solution:

Recognize the equation as a perfect square trinomial:

36 x^{2} + 36 x + 9 = (6 x)^{2} + 2 (6 x) (3) + 3^{2}

Use the formula $(a + b)^{2} = a^{2} + 2 ab + b^{2}$ :

(6 x + 3)^{2}

Final Answer:

$(6 x + 3)^{2}$

Example 5

Task:

Simplify $(3 x^{3} + 2 x^{2} - x) + (x^{3} - 4 x^{2} + 5)$

Solution:

Group and combine like terms:

(3 x^{3} + x^{3}) + (2 x^{2} - 4 x^{2}) + (- x + 5)

Simplify:

4 x^{3} - 2 x^{2} - x + 5

Final Answer:

$4 x^{3} - 2 x^{2} - x + 5$

Example 6

Task:

Simplify $(5 x^{3} - 7 x^{2} + x y - 12) - (3 x^{2} - 2 x y + x^{2})$

Solution:

Distribute the negative sign across the second polynomial:

5 x^{3} - 7 x^{2} + x y - 12 - 3 x^{2} + 2 x y - x^{2}

Combine like terms:
- $5 x^{3}$
- $- 7 x^{2} - 3 x^{2} - x^{2} = - 11 x^{2}$
- $x y + 2 x y = 3 x y$
- $- 12$

Final Answer:

$5 x^{3} - 11 x^{2} + 3 x y - 12$

Example 7

Task:

Expand $(2 x + 3) (x^{2} - x + 5)$

Solution:

Distribute $2 x$ to each term in the second polynomial:

2 x \cdot x^{2} = 2 x^{3}, 2 x \cdot - x = - 2 x^{2}, 2 x \cdot 5 = 10 x

Distribute $3$ to each term in the second polynomial:

3 \cdot x^{2} = 3 x^{2}, 3 \cdot - x = - 3 x, 3 \cdot 5 = 15

Combine like terms:

2 x^{3} + (- 2 x^{2} + 3 x^{2}) + (10 x - 3 x) + 15

Simplify:

2 x^{3} + x^{2} + 7 x + 15

Final Answer:

$2 x^{3} + x^{2} + 7 x + 15$

Example 8

Task:

Simplify $\frac{x ^{2} + x - 6}{x + 3}$

Solution:

Factor the numerator:

x^{2} + x - 6 = (x + 3) (x - 2)

Simplify by canceling the common factor $(x + 3)$ :

\frac{( x + 3 ) ( x - 2 )}{x + 3} = x - 2, x \neq = - 3

Final Answer:

$x - 2, x \neq = - 3$

Example 9

Task:

Simplify $2 x^{3} \cdot 5 x^{4} \cdot \frac{3 x ^{6}}{9 x ^{2}}$

Solution:

Multiply the coefficients and add the exponents step by step:

2 x^{3} \cdot 5 x^{4} = 10 x^{3 + 4} = 10 x^{7}

Then, the fraction:

\frac{3 x ^{6}}{9 x ^{2}} = \frac{3}{9} \cdot x^{6 - 2} = \frac{1}{3} x^{4}

Simplify:

10 x^{7} \cdot \frac{1}{3} x^{4} = \frac{10}{3} x^{7 + 4} = \frac{10}{3} x^{11}

Final Answer:

$\frac{10}{3} x^{11}$

Example 10

Task:

Simplify $(3 x^{- 2} y^{0})^{2} \cdot 3 x^{6}$

Solution:

Simplify terms symbol by symbol:
- $y^{0} = 1$ (the zero exponent rule), so we can ignore $y^{0}$ .
- Raise $(3 x^{- 2})$ to the power of $2$ :

(3 x^{- 2})^{2} = 3^{2} \cdot (x^{- 2})^{2} = 9 x^{- 4}

Rewrite the radical $3 x^{6}$ as a fractional exponent:

3 x^{6} = x^{6/3} = x^{2}

Multiply the simplified terms:

9 x^{- 4} \cdot x^{2} = 9 x^{- 4 + 2} = 9 x^{- 2}

Rewrite with positive exponents:

9 x^{- 2} = \frac{9}{x ^{2}}

Final Answer:

$\frac{9}{x ^{2}}$

Example 11

Task:

Simplify $\frac{2 x}{x ^{2} + x - 6} \cdot \frac{x + 3}{x + 2}$

Solution:

Factor the quadratic denominator $x^{2} + x - 6$ :

x^{2} + x - 6 = (x + 3) (x - 2)

Rewrite the expression:

\frac{2 x}{( x + 3 ) ( x - 2 )} \cdot \frac{x + 3}{x + 2}

Cancel the common factor $(x + 3)$ :

\frac{2 x}{( x - 2 )} \cdot \frac{1}{x + 2}

Simplify the remaining terms:

\frac{2 x}{( x - 2 ) ( x + 2 )}

Final Answer:

$\frac{2 x}{( x - 2 ) ( x + 2 )}, x \neq = - 3, x \neq = 2, x \neq = - 2$

Example 12

Task:

Simplify $11 \cdot \frac{1}{x ^{5}} \cdot 9 x^{6} y^{4}$

Solution:

Rewrite the first expression $11 \cdot \frac{1}{x ^{5}}$ :

11 \cdot \frac{1}{x ^{5}} = 11 \cdot x^{- 5}

Rewrite the radical expression $9 x^{6} y^{4}$ as exponential terms:

9 x^{6} y^{4} = (9 x^{6} y^{4})^{1/2}

Compute each term:

$(9)^{1/2} = 3$
$(x^{6})^{1/2} = x^{6/2} = x^{3}$
$(y^{4})^{1/2} = y^{4/2} = y^{2}$

Thus, $9 x^{6} y^{4} = 3 x^{3} y^{2}$ .

Multiply all terms:

11 \cdot x^{- 5} \cdot 3 x^{3} y^{2} = 11 \cdot 3 \cdot x^{- 5 + 3} \cdot y^{2}

⟹ 33 \cdot x^{- 2} \cdot y^{2} = 33 \cdot \frac{1}{x ^{2}} \cdot y^{2} = 33 \frac{y ^{2}}{x ^{2}}

Final Answer:

$33 \frac{y ^{2}}{x ^{2}}$

Example 13

Task:

Write $\frac{x ^{2} + x - 54}{x + 8}$ as a quotient and remainder

Solution:

Use polynomial long division to divide $x^{2} + x - 54$ by $x + 8$ :
- Divide the leading term $x^{2} \div x = x$
- Multiply this $x$ by $x + 8$ : $x \cdot (x + 8) = x^{2} + 8 x$
- Subtract: $(x^{2} + x - 54) - (x^{2} + 8 x) = - 7 x - 54$
- Divide the next term $- 7 x \div x = - 7$
- Multiply this $- 7$ by $x + 8$ : $- 7 \cdot (x + 8) = - 7 x - 56$
- Subtract: $(- 7 x - 54) - (- 7 x - 56) = 2$
Combine the results to express the quotient and remainder:

\frac{x ^{2} + x - 54}{x + 8} = x - 7 + \frac{2}{x + 8}

Here, $q (x) = x - 7, r (x) = 2, b (x) = x + 8$

Final Answer:

$x - 7 + \frac{2}{x + 8}$

Example 14

Task:

Simplify $- 2 (3 x^{2} y)^{2} \cdot (2 x y^{3})^{0}$

Solution:

Simplify $(2 x y^{3})^{0}$ : Any term to the power of $0$ equals $1$ . So, the expression simplifies to:

- 2 (3 x^{2} y)^{2} \cdot 1 = - 2 (3 x^{2} y)^{2}

Expand the squared term:

(3 x^{2} y)^{2} = 3^{2} \cdot (x^{2})^{2} \cdot y^{2} = 9 \cdot x^{2 \cdot 2} \cdot y^{2} = 9 x^{4} y^{2}

Multiply by $- 2$ :

- 2 \cdot 9 x^{4} y^{2} = - 18 x^{4} y^{2}

Final Answer:

$- 18 x^{4} y^{2}$

Example 15

Task:

Simplify $\frac{1}{x} - \frac{3}{2 x + 1}$

Solution:

. Find a common denominator: The denominators are $x$ and $2 x + 1$ . Use their product as the common denominator: $x (2 x + 1)$ .

Rewrite each fraction with the new denominator:

\frac{1}{x} = \frac{2 x + 1}{x ( 2 x + 1 )}, \frac{3}{2 x + 1} = \frac{3 x}{x ( 2 x + 1 )}

Combine the fractions:

\frac{1}{x} - \frac{3}{2 x + 1} = \frac{( 2 x + 1 ) - 3 x}{x ( 2 x + 1 )} = \frac{1 - x}{x ( 2 x + 1 )}

Final Answer:

$\frac{1 - x}{x ( 2 x + 1 )}$ or $\frac{1 - x}{2 x ^{2} + x}$

Free Full Length SAT Tests withOfficial-StyleQuestions

Practice with our full length adapive full testreal test-likequestions and proven300+points score boost

Common Traps & Tips in Digital SAT

⚠️ Common Traps

Incorrect distribution: Remember that $a (b + c) = ab + a c$ , not $a (b + c) = ab + c$ . For example, $3 (x + 2) = 3 x + 6$ , not $3 x + 2$ .
Cancellation errors: When simplifying fractions like $\frac{x + 5}{x + 3}$ , you cannot cancel the $x$ terms. You can only cancel factors, not terms. For example, in $\frac{( x + 1 ) ( x - 1 )}{( x + 1 )}, x \neq = - 1$ , you can cancel $(x + 1)$ to get $(x - 1)$ .
Exponent confusion: Remember that $(x + y)^{2} \neq = x^{2} + y^{2}$ . The correct expansion is $(x + y)^{2} = x^{2} + 2 x y + y^{2}$ .
Factoring mistakes: Not all quadratics factor nicely. For example, $x^{2} + 5 x + 3$ cannot be factored using integer coefficients.
Domain restrictions: When simplifying rational expressions, always check for domain restrictions. For example, $\frac{x ^{2} - 4}{x - 2} = x + 2$ only when $x \neq = 2$ .

💡 Helpful Tips for the Digital SAT

Tip 1: Use the "Plug in Numbers" Strategy

When questions are in multiple-choice format, test the options by plugging in easy values for the variables (e.g., $x = 1$ , $x = 0$ , or $x = - 1$ ), where valid.

Example: Simplify $16 x^{3} + 7 x^{2} - (5 x^{3} - 8 x^{2} + x - 6)$

If unsure how to directly simplify, plug in $x = 1$ into both the expression and the answer options.
Original expression: $16 + 7 - (5 - 8 + 1 - 6) = 31$
Find correct answer option matching $31$

Tip 2: Rewrite All Exponents and Roots as $x^{m}$

Avoid working with radicals or fractions; instead, rewrite them in exponential form for easier manipulation.
For example: $x \to x^{1/2}, \frac{1}{x ^{3}} \to x^{- 3}$
You can now use exponent rules more efficiently, such as: $x^{a} \cdot x^{b} = x^{a + b}, \frac{x ^{a}}{x ^{b}} = x^{a - b}$

Quick Practice: Test Your Skills!

Question 1

Which expression is equivalent to $2 a^{3} (a - 1) + 5 a^{4} - (a^{3} - 10)$ ?

A. $7 a^{4} - 2 a^{3} + 10$

B. $7 a^{4} - 3 a^{3} + 10$

C. $7 a^{4} - 3 a^{3} - 10$

D. $7 a^{4} - a^{3} + 10$

Solution:

Step 1: Expand the expression $2 a^{3} (a - 1)$

Distribute $2 a^{3}$ across $(a - 1)$ : $2 a^{3} (a - 1) = 2 a^{4} - 2 a^{3}$

Step 2: Rewrite the full expression with the expansion

$2 a^{4} - 2 a^{3} + 5 a^{4} - (a^{3} - 10)$

$= 2 a^{4} - 2 a^{3} + 5 a^{4} - a^{3} + 10$

$= 2 a^{4} + 5 a^{4} - 2 a^{3} - a^{3} + 10$

$= 7 a^{4} - 3 a^{3} + 10$

Final Answer: Option B is correct.

Or we can directly use $a = 1$ to verify:

The original expression is:

$2 a^{3} (a - 1) + 5 a^{4} - (a^{3} - 10) = 2 \cdot 1^{3} (1 - 1) + 5 \cdot 1^{4} - (1^{3} - 10) = 0 + 5 - (1 - 10) = 14$

Next, we plug $a = 1$ into each option:

For A: $7 a^{4} - 2 a^{3} + 10 = 7 \cdot 1^{4} - 2 \cdot 1^{3} + 10 = 7 - 2 + 10 = 15$ , which is $\neq = 14$ , so it's wrong.
For B: $7 a^{4} - 3 a^{3} + 10 = 7 \cdot 1^{4} - 3 \cdot 1^{3} + 10 = 7 - 3 + 10 = 14$ , which is $= 14$ , so it's possible to be true.
For C: $7 a^{4} - 3 a^{3} - 10 = 7 \cdot 1^{4} - 3 \cdot 1^{3} - 10 = 7 - 3 - 10 = - 6$ , which is $\neq = 14$ , so it's wrong.
For D: $7 a^{4} - a^{3} + 10 = 7 \cdot 1^{4} - 1^{3} + 10 = 7 - 1 + 10 = 16$ , which is $\neq = 14$ , so it's wrong.

Since only Option B matches 14, it's the correct answer.

Question 2

Which expression is equivalent to $50 π^{3} \cdot 3 π^{6}$ ?

A. $50 π$

B. $50 π^{5}$

C. $50 π^{\frac{3}{2}}$

D. $50 π^{6}$

Solution:

Step 1: Simplify the cube root ( $3 π^{6}$ )

3 π^{6} = π^{\frac{6}{3}} = π^{2}

So the given expression becomes:

50 π^{3} \cdot π^{2}

Step 2: Use the rule of exponents ( $a^{m} \cdot a^{n} = a^{m + n}$ )

Combine the powers of $π$ :

50 π^{3} \cdot π^{2} = 50 π^{3 + 2} = 50 π^{5}

Final Answer: Option B is correct.

Question 3

Which of the following expression is equivalent to $\frac{x ^{2} + 3 x - 10}{x - 2}$ for $x \neq = 2$ ?

A. $x + 5$

B. $x + 5 - \frac{10}{x - 2}$

C. $x + 5 + \frac{10}{x - 2}$

D. $x + 5 + \frac{20}{x - 2}$

Solution:

Factor the numerator: $x^{2} + 3 x - 10 = (x + 5) (x - 2)$

Now we can simplify:

$\frac{x ^{2} + 3 x - 10}{x - 2} = \frac{( x + 5 ) ( x - 2 )}{x - 2} = x + 5$ , $x \neq = 2$

The answer is Option A.

Or we can plug $x = 3$ into the expressions to find out which option is true:

The original expression is: $\frac{x ^{2} + 3 x - 10}{x - 2} = \frac{3 ^{2} + 3 \cdot 3 - 10}{3 - 2} = 8$

Next, we plug $x = 3$ into the given options:

For A: $x + 5 = 3 + 5 = 8$ , which is $= 8$ , so it's possible to be true.
For B: $x + 5 - \frac{10}{x - 2} = - 2$ , which is $\neq = 8$ , so it's wrong.
For C: $x + 5 + \frac{10}{x - 2} = 18$ , which is $\neq = 8$ , so it's wrong.
For D: $x + 5 + \frac{20}{x - 2} = 28$ , which is $\neq = 8$ , so it's wrong.

Since only Option A matches $8$ , it's the correct answer.

Question 4

If $m = 7 x - 5$ and $n = x^{2} + 2$ , which of the following is equivalent to $mn - n$ ?

A. $7 x^{3} - 5 x^{2} + 14 x - 12$

B. $7 x^{3} - 6 x^{2} + 14 x - 8$

C. $7 x^{3} - 6 x^{2} + 14 x - 12$

D. $7 x^{3} - 5 x^{2} - 14 x - 10$

Solution:

$mn - n = n (m - 1) = (x^{2} + 2) (7 x - 5 - 1)$

$⟹ (x^{2} + 2) (7 x - 6) = x^{2} \cdot 7 x + x^{2} \cdot (- 6) + 2 \cdot 7 x + 2 \cdot (- 6)$

$⟹ 7 x^{3} - 6 x^{2} + 14 x - 12$

The answer is Option C.

Or we can plug $x = 1$ into the expressions to find out which option is true:

$m = 7 \cdot 1 - 5 = 2$ and $n = x^{2} + 2 = 1^{2} + 2 = 3$ , so: $mn - n = 2 \cdot 3 - 3 = 3$

Next, we plug $x = 1$ into the given options:

For A: $7 x^{3} - 5 x^{2} + 14 x - 12 = 4$ , which is $\neq = 3$ , so it's wrong.
For B: $7 x^{3} - 6 x^{2} + 14 x - 8 = 7$ , which is $\neq = 3$ , so it's wrong.
For C: $7 x^{3} - 6 x^{2} + 14 x - 12 = 3$ , which is $= 3$ , so it's possible to be true.
For D: $7 x^{3} - 5 x^{2} - 14 x - 10 = - 22$ , which is $\neq = 3$ , so it's wrong.

Since only Option C matches $3$ , it's the correct answer.

Question 5

10 x^{3} - 5 x^{2} - 5 x

The given expression is equivalent to $a x (x - 1) (b x + 1)$ , where $a$ and $b$ are constants. What is the value of $b$ ?

Solution:

Step 1: Factor out the common term in the polynomial

The given polynomial $10 x^{3} - 5 x^{2} - 5 x$ has $5 x$ as a common factor. So, we factor it out:

10 x^{3} - 5 x^{2} - 5 x = 5 x (2 x^{2} - x - 1)

Step 2: Factorize the quadratic $2 x^{2} - x - 1$

Identify the coefficients:

$a = 2$ (coefficient of $x^{2}$ )
$b = - 1$ (coefficient of $x$ )
$c = - 1$ (constant term)

Find two numbers that multiply to $a \cdot c = 2 \cdot (- 1) = - 2$ and add to $b = - 1$ :

The numbers are $- 2$ and $1$ .

Split the middle term using these numbers:

2 x^{2} - x - 1 = 2 x^{2} - 2 x + x - 1

Group the terms in pairs and factorize:

(2 x^{2} - 2 x) + (x - 1) = 2 x (x - 1) + 1 (x - 1)

Factor out the common binomial $(x - 1)$ :

2 x^{2} - x - 1 = (2 x + 1) (x - 1)

Step 3: Rewrite the full factorization

Substitute the factored quadratic $(2 x + 1) (x - 1)$ back into the polynomial:

10 x^{3} - 5 x^{2} - 5 x = 5 x (2 x + 1) (x - 1)

Step 4: Compare with the given form

The given form of the expression is:

From the factorization, we can identify:

$a = 5$
$b = 2$

Final Answer: The value of $b$ is $2$ .

Your Turn! Realistic "Equivalent Expressions" Questions for DSAT Success

Question 1

Difficulty level: Easy

Which expression is equivalent to $158 t^{3} - 24 t^{2} u$ ?

A. $2 t (79 t^{2} - 12 u)$

B. $2 t^{2} (79 t - 12 u)$

C. $2 t u (79 t^{2} - 12)$

D. $2 t^{2} u (79 t - 12)$

Question 2

Difficulty level: Medium

The expression $72 y^{5} - 48 y^{4}$ is equivalent to $r y^{4} (12 y - 8)$ , where $r$ is a constant. What is the value of $r$ ?

Question 3

Difficulty level: Hard

Which of the following expressions has a factor of $x + 2 b$ , where $b$ is a positive integer constant?

A. $2 x^{2} + 5 x + 10 b$

B. $2 x^{2} + 15 x + 10 b$

C. $2 x^{2} + 20 x + 10 b$

D. $2 x^{2} + 25 x + 10 b$

"Equivalent Expressions" Learning Checklist

🔘 Master factoring $a x^{2} + b x + c$
- Always reduce the coefficient of $x^{2}$ to 1 if possible.
- Factor out common terms first. Simplify whenever possible.
- Use the grouping method for factoring
🔘 Memorize special factoring rules:
- Square of a Sum $a^{2} + 2 ab + b^{2} = (a + b)^{2}$
- Square of a Difference $a^{2} - 2 ab + b^{2} = (a - b)^{2}$
- Difference of Squares $a^{2} - b^{2} = (a + b) (a - b)$
🔘 Be familiar with the common integer square table.
🔘 Understand what is an exponential expression: $a x^{m}$
🔘 Be aware of the difference between $a x^{m}$ and $(a x)^{m}$
🔘 Master the rules of exponent operations proficiently:
- $a x^{m} + b x^{m} = (a + b) x^{m}$
- $a x^{m} - b x^{m} = (a - b) x^{m}$
- $a^{m} \cdot a^{n} = a^{m + n}$
- $\frac{a ^{m}}{a ^{n}} = a^{m - n}$ , $a \neq = 0$
- $(a^{m})^{n} = a^{m \cdot n}$
- $a^{- m} = \frac{1}{a ^{m}}$ , $a \neq = 0$
- $a^{0} = 1$ , $a \neq = 0$
- $n a^{m} = a^{\frac{m}{n}}$
🔘 Understand polynomials of different quantities of terms such as $5 x^{2}, x^{3} - y^{2}, x^{3} - x + 10$
🔘 Master how to add or subtract polynomials:
- what are "like terms"
- how to combine them(only the coefficients change)
🔘 Master how to multiply polynomials:
- Multiply each term in one polynomial by each term in the other polynomial, such as $a x (x + b) = a x \cdot x + a x \cdot b$
- Use the FOIL method for binomials, $(a x + b) (c x + d)$ = $a x \cdot c x + a x \cdot d + b \cdot c x + b \cdot d$
- When multiplying terms that have the same base: multiply the coefficients, keep the base the same and add the exponents, such as: $a x^{m} \cdot b x^{n} = a \cdot b \cdot x^{m + n}$
🔘 Master two core steps to simplify a rational expression:
- Factor the numerator and denominator completely
- Cancel common factors
🔘 Master operations with rational expressions by using the same rules as fractions.
🔘 Learn and practice polynomial long division to rewrite rational expressions as quotients and remainders: $q (x) + \frac{r ( x )}{b ( x )}$ , where $r (x)$ is the remainder.
🔘 Making good use of the numerical substitution method, like $x = 0$ , $x = 1$ , to solve problems quickly, which is a very practical approach in real SAT.

Essential SAT Prep Tools

Maximize your SAT preparation with our comprehensive suite of tools designed to enhance your study experience and track your progress effectively.

Personalized Study Planner

Get a customized study schedule based on your target score, available study time, and test date.

Create Study Plan

Expert-Curated Question Bank

Access 2000+ handpicked SAT questions with detailed explanations, organized by topic and difficulty level.

Explore Question Bank

Smart Flashcards

Create and study with AI-powered flashcards featuring spaced repetition for optimal retention.

Start with Flashcards

Score Calculator

Convert raw scores to scaled scores instantly and track your progress towards your target score.

Calculate Your Score

SAT Skills Lessons

Master each SAT skill with progressive lessons and comprehensive guides, from foundational concepts to advanced techniques.

Start Learning

Full-Length Practice Tests

Experience complete SAT exams under realistic conditions with adaptive difficulty.

Start Full Test

Pro Tip

Start your SAT prep journey by creating a personalized study plan 3-4 months before your test date. Use our time management tools to master pacing, combine mini-tests for targeted practice, and gradually progress to full-length practice tests. Regular review with flashcards and consistent practice with our question bank will help you stay on track with your study goals.

Best Digital SAT Math Prep: "Equivalent Expressions"

Frontier Lesson: "Equivalent Expressions" for the Digital SAT

How to Factor Quadratic and Polynomial Expressions?

🟠 Step 1: If possible, reduce the coefficient of x2 to 1

🟠 Step 2a: Factor x2+bx+c (when the coefficient of x2=1)

🟠 Step 2b: Factor ax2+bx+c (when the coefficient of x2 is not 1)

🟠 Special Factoring Rules

➤ (a) Square of a Sum

➤ (b) Square of a Difference

➤ (c) Difference of Squares

➤ Final Steps for Factoring Quadratics

🟠 Common Integer Square Table

Free Full Length SAT Tests withOfficial-StyleQuestions

Exponential Expressions & Operations with Polynomials

🟠 Common Types of Polynomials in SAT Questions:

🟠 How to Add or Subtract Polynomials

➤ a. Combine Like Terms

➤ b. Combine Only the Coefficients

➤ c. Be Mindful of Parentheses and Signs

➤ d. Write Expressions in Descending Order of Exponents

🟠 How to Multiply Polynomials

➤ a. Distribute Terms When Multiplying Polynomials

➤ b. Use the FOIL Method for Binomials

➤ c. Multiplying Terms with the Same Base

🟠 What Is an Exponential Expression?

🟠 The Rules of Exponent Operations

➤ a. Adding and Subtracting Exponential Expressions

➤ b. Multiplying Exponential Expressions

➤ c. Dividing Exponential Expressions

➤ d. Raising an Exponential Expression to an Exponent

➤ e. Negative Exponents

➤ f. Zero Exponent

➤ g. Rewriting Roots as Rational Exponents

How to Do Operations with Rational Expressions

🟠 What Are Rational Expressions?

🟠 How to Simplify Rational Expressions

Steps to Simplify a Rational Expression:

🟠 How to Add or Subtract Rational Expressions

🟠 How to Multiply or Divide Rational Expressions

➤ a. Multiplying Rational Expressions

➤ b. Dividing Rational Expressions

➤ c. Factor First to Simplify Multiplication and Division

🟠 How to Rewrite Rational Expressions as Quotients and Remainders

Worksheet for Building Mastery in Algebraic Operations

Example 1

Example 2

Example 3

Example 4

Example 5

Example 6

Example 7

Example 8

Example 9

Example 10

Example 11

Example 12

Example 13

Example 14

Example 15

Free Full Length SAT Tests withOfficial-StyleQuestions

Common Traps & Tips in Digital SAT

⚠️ Common Traps

💡 Helpful Tips for the Digital SAT

Quick Practice: Test Your Skills!

Question 1

Question 2

Question 3

Question 4

Question 5

Your Turn! Realistic "Equivalent Expressions" Questions for DSAT Success

Question 1

Question 2

Question 3

"Equivalent Expressions" Learning Checklist

Essential SAT Prep Tools

Personalized Study Planner

Expert-Curated Question Bank

Smart Flashcards

Score Calculator

SAT Skills Lessons

🟠 Step 1: If possible, reduce the coefficient of $x^{2}$ to 1

🟠 Step 2a: Factor $x^{2} + b x + c$ (when the coefficient of $x^{2} = 1$ )

🟠 Step 2b: Factor $a x^{2} + b x + c$ (when the coefficient of $x^{2}$ is not 1)